本文涉及：量子力学、线性代数、概率论、密码学

本文仅阐述概念，不解释原理。

这篇blog会一直更新、缓慢更新，一直缓慢更新。

下文涉及的“经典”二字，只是（初中涉猎量子力学导致的）个人嗜好，其实原文是classical，译作“古典”更为合适。（经典对应的单词是classic）

欢迎捉虫

1. Turing machine

图灵机

2.Qubit

量子比特

2.1.单个量子比特

一个量子比特有两种计算上的基本状态：$|0\rangle$ 和 $|1\rangle$

但与经典比特不同的地方在于，量子比特可以处于这两种状态之外，通常称作叠加态，表示为：

$|\psi\rangle = \alpha|0\rangle+\beta|1\rangle$

其中 $\alpha$ 和 $\beta$ 落在复数域中（不过把它们看作是实数也不会有什么损失）

量子力学告诉我们，当测量一个量子比特的时候，它会以概率 $|\alpha|^2$ 的概率坍缩为 0 ；以概率 $|\beta|^2$ 的概率坍缩为1.

因为 $|\alpha|^2 + |\beta|^2 = 1$（显然概率和为1），所以 $|\psi\rangle$ 的模长恒为1

因此可以说一个量子比特的状态相当于落在二维复数向量空间的一个单位向量。

举个例子，一个量子比特可以处于如下状态(在被测量到之前)：

$\frac{1}{\sqrt2} |0\rangle+\frac{1}{\sqrt2}|1\rangle$

测量时，它会以$(1/\sqrt2)^2$ 的概率（即50%）坍缩为0，以$(1/\sqrt2)^2$ 的概率（即50%）坍缩为1。

这样的量子比特通常被记作$|+\rangle$

即 $|+\rangle = \frac{1}{\sqrt2} |0\rangle+\frac{1}{\sqrt2}|1\rangle$

2.2.多个量子比特

两个经典比特可以有如下状态：

00，01，10，11

相应地，一个由两个量子比特组成的系统也有4种*“计算上的基本状态”*：

$|00\rangle,|01\rangle,|10\rangle,|11\rangle$

当然，两个量子比特同样可以处于这四种状态的叠加态，因此由两个量子比特组成的状态向量可以表示为：

$|\psi\rangle = \alpha_{00}|00\rangle+\alpha_{01}|01\rangle+\alpha_{10}|10\rangle+\alpha_{11}|11\rangle$

跟上文一样，测量结果x = (00,01,10,11)以概率$|\alpha_x^2|$

出现，且

$\sum_{x\in\{0,1\}^2}|\alpha_x|^2=1$

其中符号 $\{0,1\}^2$ 表示长度为2的字符串集合，每个字可能为0，或者为1

对于由两个量子比特组成的系统，我们可以仅仅测量它的子集，比如说只测量第一个qubit，它的结果为0的概率为：

$|\alpha_{00}|^2+|\alpha_{01}|^2$

在这个前提下，$|\psi \rangle$ 只剩下两种可能性 $|00\rangle,|01\rangle$

因此状态向量转变为：

$|\psi'\rangle = \frac{\alpha_{00}|00\rangle+\alpha_{01}|01\rangle}{\sqrt{|\alpha_{00}|^2+|\alpha_{01}|^2}}$

这个式子怎么来的，以下是我的思考：

在第一个qubit已知为0的前提下，显然只剩下两种可能性 $|00\rangle,|01\rangle$

那么它们的概率分别是多少？（注意，现在这两种情况的概率和为1）

由于事件的可能性从一般的4种变为了2种，这个问题的答案我们暂时不知道，但我们知道的是它们的概率之比——依旧为 $\alpha_{00}^2 : \alpha_{01}^2$

设其中的一个概率为x，另一个则为 (1-x)

那么有 $x:(1-x) = \alpha_{00}^2 : \alpha_{01}^2$

很容易就得到上面的式子了。

当然，该式子是基于第一个qubit（坍缩后）的状态与第二个qubit无关的情况下推导出来的。

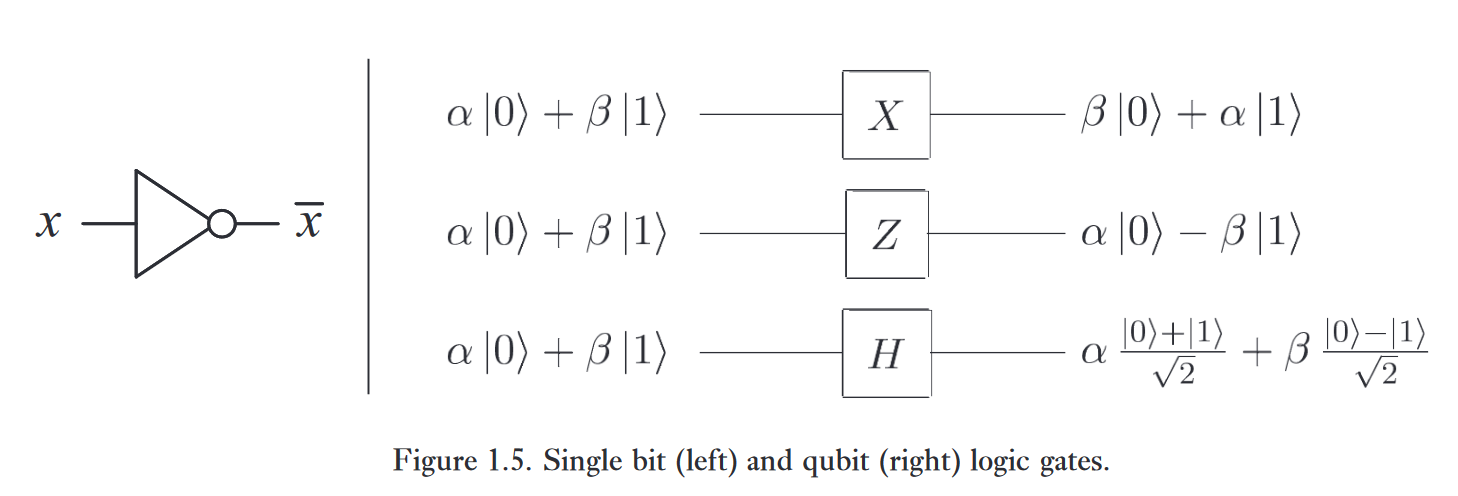
2.3.单量子比特门

single qubit gates

从非门开始讲起（事实上，在经典世界，单比特门只有非门一种非平凡门）：

在经典电路中，非门输入0输出1；输入1输出0，也就是0与1状态交换了。

而量子非门略有不同，它将$\alpha |0\rangle+\beta|1\rangle$ 作为输入，输出 $\beta|0\rangle + \alpha|1\rangle$

也就是说，量子非门是一种线性操作。

实际上，由于量子力学，所有的量子门都是线性门。（否则就会出现时间旅行、超越光速等矛盾现象）

所以自然可以构造如下矩阵来表示量子非门：

$X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$

于是有

$X\begin{bmatrix} \alpha \\ \beta \end{bmatrix} = \begin{bmatrix} \beta \\ \alpha \end{bmatrix}$

事实上，所有作用与单个量子的量子门都可以用二维矩阵表示，为了使得经过量子门后$|\alpha'|^2+|\beta'|^2=1$依然成立，这些二维矩阵 $U$ 满足：

$U^\dagger U = I$

其中 $U^\dagger$ 是 $U$ 的共轭转置，$I$是单位矩阵

此时，$U$ 被称作幺正矩阵

令人惊喜的是，除了以上性质，没有别的因素能够限制一个 $U$ 的构造了

这个结论告诉我们，在量子世界，单比特门并非只有非门一种非平凡门（实际上有无限多种）。

比方说两个很重要的门：

• Z门：

$Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$

让 $|0\rangle$ 保持不变，$|1\rangle$ 变为 $-|1\rangle $

• Hadamard 门：

$H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$

它让 $|0\rangle$ 变成$ (|0\rangle+|1\rangle)/\sqrt2$ ，让 $|1\rangle$ 变成 $(|0\rangle-|1\rangle)/\sqrt2$

不难发现 $H^2 = I$

2.3.1.幺正矩阵的分解

前文提到，2x2的幺正矩阵有无限多个，意味着合法的单量子比特门有无限多个。但惊喜的是，任意的幺正矩阵都可以分解为：

$U = e^{i\alpha}\begin{bmatrix} e^{-i\beta/2} & 0 \\ 0 & e^{i\beta/2} \end{bmatrix}\begin{bmatrix} cos\frac{\gamma}{2} & -sin\frac{\gamma}{2} \\ sin\frac{\gamma}{2} & cos\frac{\gamma}{2} \end{bmatrix}\begin{bmatrix} e^{-i\delta/2} & 0 \\ 0 & e^{i\delta/2} \end{bmatrix}$

其中$\alpha,\beta,\gamma,\delta$ 是实数。

这个结论告诉我们，一个任意的单量子比特门可以用有限个量子门的集合来构造（实际上，多量子也可以）

2.4.多量子比特门

常见的多经典比特门有如下几种：

与门、或门、异或门、与非门、或非门。

2.4.1.量子不可克隆

量子力学告诉我们，量子不可克隆（copy）

所以量子电路不支持FANOUT

3.计算复杂度

参考

[1] Quantum Computation and Quantum Information