本文是对超奇异椭圆曲线同源密钥协商理论研究的工程向补充

在SIDH受攻击后，本文已过时。

0.关键操作

0.复数运算（ $F_{p^2}$ 里的任意元素长这样: $u+vi$ , 其中 $u,v \in F_p$ , $i^2 = -1$ ）

1.素数判定（p是否为素数）

2.超奇异判定（E是否为超奇异椭圆曲线）

3.j-invariant计算

4.Weil pairing计算（为了检验P与Q是否线性无关）

5.倍点、点加、随机点的选取

6.复数运算

7.计算挠群

8.根据kernel计算同源映射(Velu’s formula)

9.等等……

SIDH最核心的一步就是计算同源（也是前量子公钥密码没有的操作）

同源本质上是一个态射，是一个比较抽象的“东西”，那么怎么构造它呢？

所幸我们有Velu’s formula

0.1.Velu’s formula确定isogeny

以下是利用Velu’s formula计算isogeny的过程

0.1.0.准备工作

通过同构映射:

$\phi(x,y) = (\frac{x}{b},\frac{y}{b^2})$

构造与SIDH所用曲线(Montgomery Form)：

$E_0:by^2 = x^3 + ax^2 + x$

同构的曲线(Weierstrass Form)：

$E_1:y^2+axy+by = x^3 + cx^2 + dx + e$

与kernel:

G,一个 $E_1$ 的子群

0.1.1.分割G

1.丢弃单位元O

2.构造 $G_2$ 为 G[2]，即G的2-挠群，R为剩下所有点的集合

3*.二等分R，分别命名为 $R_+,R_-$ ，如果 $P \in R_+$ , 那么 $-P \in R_-$

0.1.2.计算系数

1.令 $S = R_+ \cup G_2,Q =(x_Q,y_Q) \in S$ ，计算：

$f_Q = 3x_Q^2 + 2cx_Q + d - ay_Q$
$g_Q = -2y_Q-ax_Q-b$
如果 $Q \in G_2$ , 令 $v_Q = f_Q$ ，否则令 $v_Q = 2f_Q-ag_Q$
令 $u_Q = (g_Q)^2$
计算 $v = \sum_{Q\in S}v_Q,w=\sum_{Q\in S}(u_Q+x_Qv_Q)$

0.1.3.构造codomain

$A = a$

$B = b$

$C = c$

$D = d-5v$

$E = e-(a^2+4c)v-7w$

得到 $E_2:y^2+Axy+By = x^3+Cx^2+Dx+E$

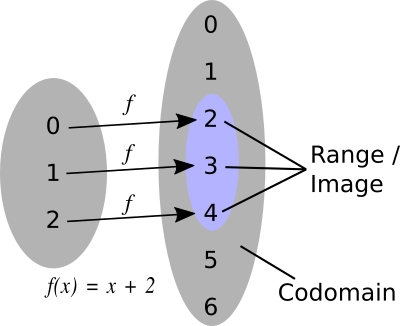
图为Codomain和Image的区别，不过在SIDH中这两个相等，因为isogeny是满射（surjective）。

0.1.4.计算image

由上得到一个isogeny

$\Phi: E_1 \rightarrow E_2$

使得对 $E_1$ 中任意一点Q有：

$\Phi(x,y) = (\alpha,\beta)$

其中

$\alpha = x+\sum_{Q\in S}(\frac{v_Q}{x-x_Q}-\frac{u_Q}{(x-x_Q)^2})$

$\beta = y - \sum_{Q\in S}(u_Q\frac{2y+ax+b}{(x-x_Q)^3}+v_Q\frac{a(x-x_Q)+y-y_Q}{(x-x-Q)^2}+\frac{au_Q-f_Qg_Q}{(x-x_Q)^2})$

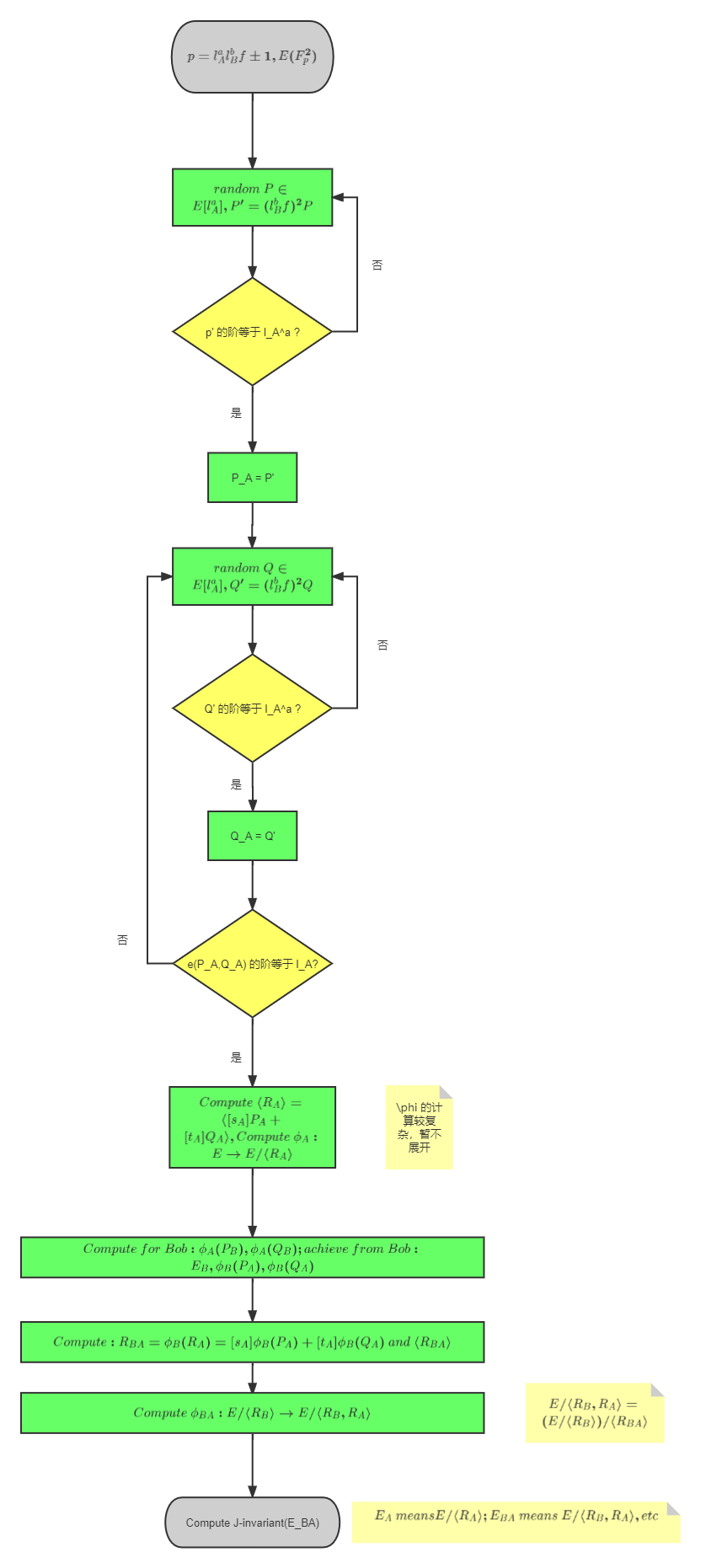
1.程序流程图

我少有画程序流程图的经验，欢迎指正。

以下是Alice的操作，Bob与之类似

2.Sagemath代码展示

这里的代码搬自bintou的博客，有极少量的修改

2.1.参数设置

#选取一条在素域k上的超奇异椭圆曲线，这里f = 1
lA, lB = 2, 3
eA, eB = 6, 7
p = lA ^ eA * lB ^ eB - 1
assert p.is_prime()
assert p % 4 == 3
k = GF(p) # 注意，这里并不是标准做法，只是因为Sage的局限不得已;
E = EllipticCurve(k, [1, 0]) #选取曲线
E
E.is_supersingular() # 看看所生成的曲线是否超奇异.
E.j_invariant()

#选取四个随机点作为公共参数
points = []
while len(points) != 4:
    p = E.random_point()
    if p not in points:
        points.append(p)
PA, PB, QA, QB = points
PA, PB, QA, QB

2.2.Alice的操作

#Alice选择两个随机数并计算自己的秘密值RA
#RA定义了phi_A的kernel
sA, tA = 123, 525
RA = sA * PA + tA * QA
print(RA)

#phiA就是同源也是群同态
phiA = E.isogeny(RA)

#Alice的公共信息EA
EA = phiA.codomain()
print(E.is_isogenous(EA)) # 确认EA与E同源.

#Alice发送以下值给Bob
EA, phiA_PB, phiA_QB = EA, phiA(PB), phiA(QB)
EA, phiA_PB, phiA_QB

2.3.Bob的操作

#Bob的工作类似
sB, tB = 812, 580
RB = sB * PB + tB * QB
print(RB)

# phiB就是从E到EB同态映射,Kernel是RB
phiB = E.isogeny(RB)
print(phiB)
EB = phiB.codomain()
print(EB)
print(E.is_isogenous(EB))

# Bob发送以下信息给Alice:
EB, phiB_PA, phiB_QA = EB, phiB(PA), phiB(QA)
EB, phiB_PA, phiB_QA

2.4.秘密值计算

# Alice计算秘密值
R_BA = sA * phiB_PA + tA * phiB_QA
print(R_BA)
phiBA = EB.isogeny(R_BA)
print(phiBA)
KA = phiBA.codomain().j_invariant()

# Bob计算秘密值
R_AB = sB * phiA_PB + tB * phiA_QB
print(R_AB)
phiAB = EA.isogeny(R_AB)
print(phiAB)
KB = phiAB.codomain().j_invariant()

#测试秘密值是否相等
if KA == KB:
    print("Success!")

3.各种来源的代码分析

3.0.C/Cython/Python/Sagemath缝合代码

defeo/ss-isogeny-software: Software for “Quantum-Resistant Cryptosystems from Supersingular Elliptic Curve Isogenies” (github.com)

链接内含 SIDH创始人之一De Feo 撰写的代码，融合了C/Cython/Python/Sagemath。

sagemath负责参数生成，python负责同源计算策略的计算，C负责关键算术运算（利用GMP库），密钥交换于Cython内完成

3.1.sidh-crypto的代码

是github上的organization，具体成员没有公开，但不难发现SIDH创始人之一David Jao是其中之一。

sidh-crypto (github.com)

以下主要分析它的C代码sidh-crypto/sidh-c-reference: SIDH C reference implementation，为行文方便，文件名只截取了最后一部分。

包括密钥协商和加解密（SIKE?）两大部分，暂只分析密钥协商部分。

clear等释放内存的函数就不提及了

dlp.h: solve ECDLP

由于SIDH选取的素数p，减1后的 p-1属于smooth number，所以其ECDLP问题可以用Pohlig–Hellman algorithm解决。

curve.h:

曲线相关

输入参数a和b，构造椭圆曲线：y^2 = x^3 + a * x^2 + b * x + c（这里选用的是Weierstrass form曲线，且域特征不等于2或3，且c=0）
求j-invariant
判断点是否落在曲线上

点相关

生成零点、设置零点（即无穷远点）
指定生成一点（射影坐标，即有xyz三个参数）
令Q = P
判断点是否为零点（即无穷远点，z==0）
求逆元，即输入(x,y)输出(x,-y)
判断点的阶是否为2
判断两点是否相等
点加,有两种：输入有斜率；输入无斜率
点减，即input:P,Q ; output:P+(-Q)
倍点，有2倍点和任意倍
随机生成一点

public_param.h

公共参数相关的函数

初始化公共参数（给它们赋值0）
从文件中读取公共参数
输出公共参数： $p,E,l_A,e_A,l_B,e_B$

private_key.h

根据公钥生成私钥，大概就是由P和Q得到kernel的生成元R = [m]P+[n]Q,其中 $m\ mod\ l^e$ 存在逆元

isogeny.h

用生成元计算isogeny
把domain的点P 同源映射到codomain上，有两种方法：velu和kohel
计算kernel的partition
计算共享曲线E，有两种：naive和strategy，naive的最后大概要650000ms，strategy的话大概是250000ms

3.2.Microsoft的代码

microsoft/PQCrypto-SIDH

微软在GitHub上的开源软件仓库中的代码，还没看

4.运行时间测量与比较

运行环境：WSL2 c语言

该密钥生成方案并不快（相比对称密码和传统DH），我参考了知乎的说法，选用了<time.h>的clock_gettime()来测量运行时间时间测量方法？- 知乎 (zhihu.com)

以下是一个demo

/*
gcc -O2 testtime.c -o testtime.out -static
./testtime.out
*/
#include<time.h>
#include<stdio.h>
#include<stdlib.h>

#define MILLION 1000000

int main(void)
{
        long int loop = 1000;
        struct timespec tpstart;    
        struct timespec tpend;
        long timedif;					

        clock_gettime(CLOCK_MONOTONIC, &tpstart);
		/*以下看作某个加密函数*/
        while (--loop){
                system("cd");
        }

        clock_gettime(CLOCK_MONOTONIC, &tpend);
        timedif = MILLION*(tpend.tv_sec-tpstart.tv_sec)+(tpend.tv_nsec-tpstart.tv_nsec)/1000;
        fprintf(stdout, "it took %ld microseconds\n", timedif);

        return 0;
}

最后会输出一段代码运行消耗的微秒数(microseconds)

但在我把它套在test_key_exchange上时（sidh-crypto的代码），发现报错:

1	error: ‘CLOCK_MONOTONIC’ undeclared

在头文件前面加上这个宏定义就好了（可能是gcc版本问题？

1	#define _POSIX_C_SOURCE 199309L

最后我测出来key_exchange的时间大概是（只是本地执行密钥交换的时间，公共参数初始化没算在内，用了**-O2**）

略大于 250000 ms（0.25秒）

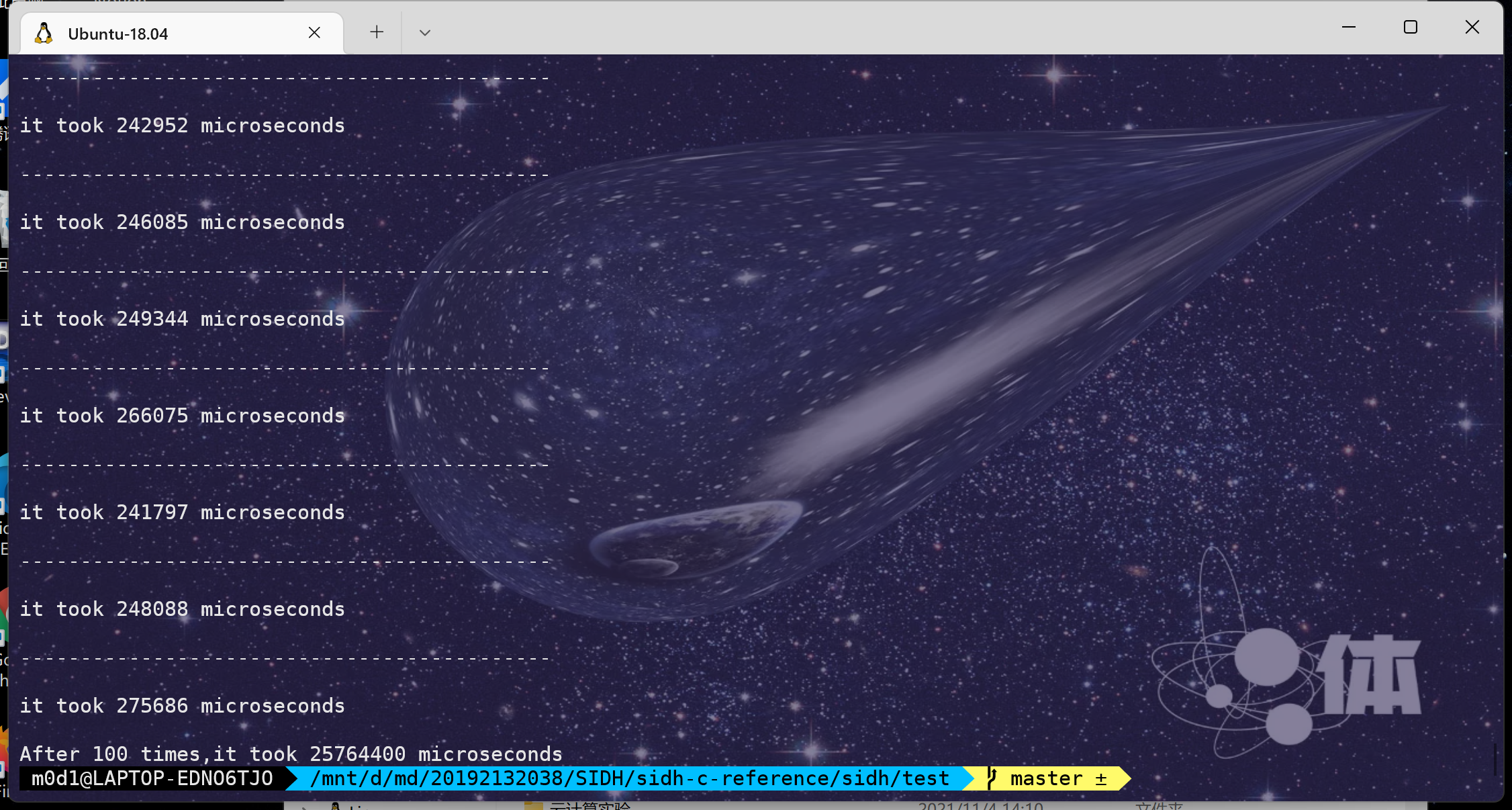
在github上（随便）找了个ECDH的实现

kokke/tiny-ECDH-c

测了一下它的速度100次，同样用的是 -O2 ：

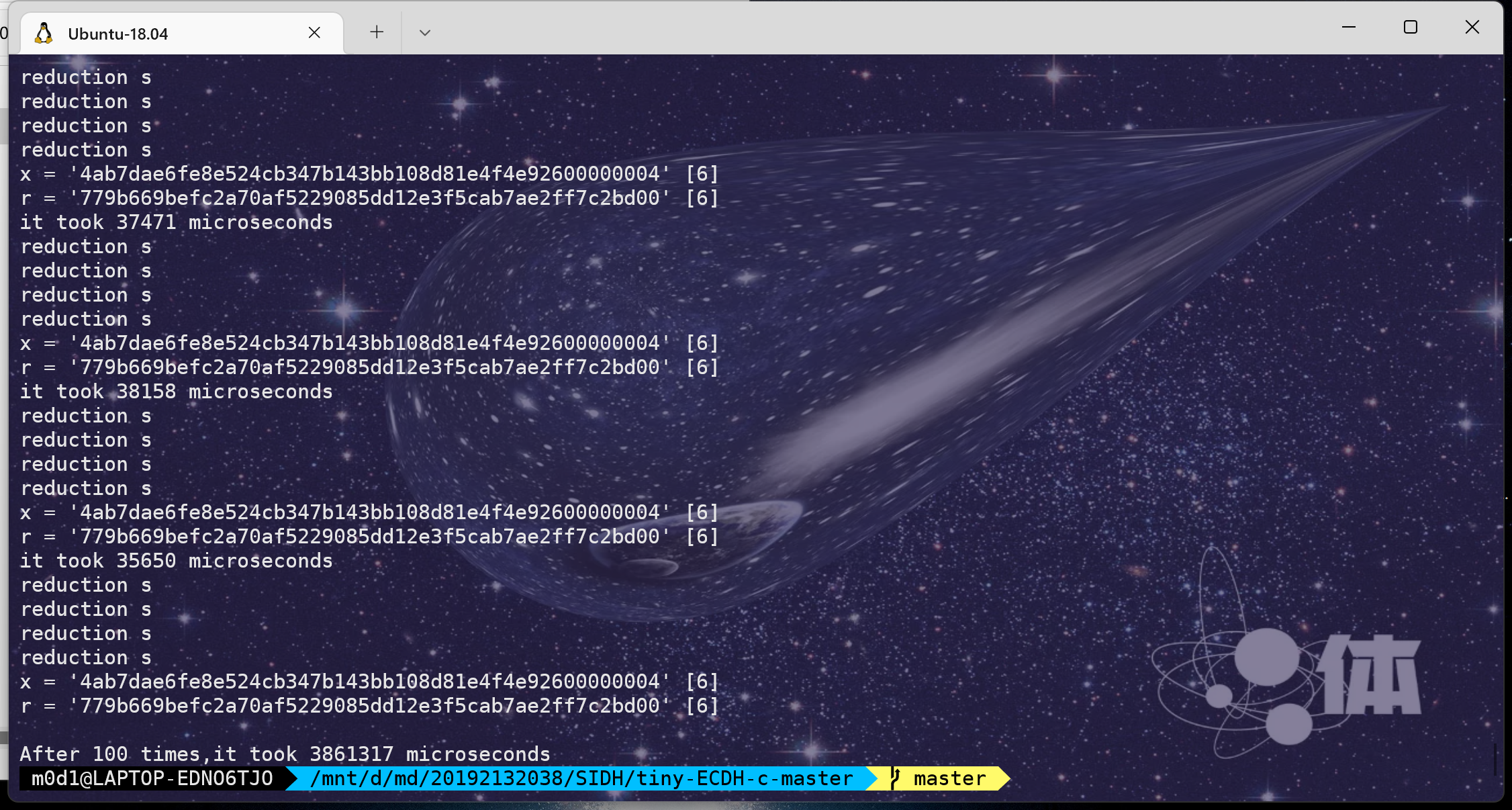
平均 38613.17 ms（0.038秒）

可以发现差距还是很大的，相差一个数量级。

5.优化方向

摘自[6]:目前，对于SIDH的优化计算主要从以下3个角度来展开：探索适合的域的形式；借助不同曲线形式、不同坐标形式的优势；利用一些特殊技巧，如加法链、Weil限制和双线性对等去优化

具体而言，有

（1）有限域的运算：任何加速底层的有限域的基本算术方法都能加快SIDH的实现。

（2）标量乘：即倍点运算

（3）曲线以及坐标的类型：不同的曲线模型以及不同的坐标形式，其上的点加、倍点、同源和同源曲线的代数操作的计算量是不同的

（4）同源和同源曲线的计算：在SIDH中，Alice和Bob均需要计算 $l^e$ -同源和同源曲线。对于 $l^e$ -同源的计算，需要进行e次 $l$ -同源的复合。显然复合次数越少，计算速度越快。对于同源曲线的计算，当 $l$ 较大时，直接利用同源曲线公式计算效率较低。

（5）压缩公钥和恢复公钥的计算量：暂时忽略。

6.毕设相关

大概的毕设思路

第一章椭圆曲线及其倍点运算介绍

第二章 SIDH的理论解析

第三章 SIDH的代码实现

第四章 SIDH的后续优化

第五章结论

参考

[1] 后量子安全密钥交换协议SIDH简介 | Bintou’s Blog

[2] Efficient Implementations of A Quantum-Resistant Key-Exchange Protocol on Embedder systems

[3] Efficient algorithms for supersingular isogeny Diffie-Hellman

[4] A Friendly Introduction to Supersingular Isogeny Diffie-Hellman

[5] Vélu’s Formulas for SIDH - Maria Corte-Real Santos (mariascrs.com)

[6] 椭圆曲线同源的有效计算研究进展

[7] Quantum Computation and Quantum Information