利用中国剩余定理(CRT)和欧拉定理求解模指数运算问题

留意 ’ = ’ 和 ’ ≡ ’ 的转换时机

前置知识请看：中国剩余定理指北 | M0D1.TOP

(1) 手动计算 $2000^{2019} (mod\ 221)$

解：

221 = 17*13

由中国剩余定理得

$2000^{2019} mod\ 221 \cong ([11^{2019} mod\ 17],[11^{2019}mod\ 13])$

由欧拉定理：

$11^{\phi (17)} = 11^{16} ≡ 1\ mod\ 17$

$∴ 11^{2019} = 11^{16*126+3} ≡ 11^{3} ≡ 5\ (mod\ 17)$

又 $11^{\phi (13)} = 11^{12}≡ 1\ mod\ 13$

$∴ 11^{2019} = 11^{12*168+3} ≡ 11^{3} ≡ 5\ (mod\ 13)$

令

$x ≡ 5\ (mod\ 17)$

$x ≡ 5\ (mod\ 13)$

再次运用中国剩余定理得:

(由于式子很特殊这一步多此一举，但是为了鲁棒性我还是写了)

$x ≡ 5\ mod\ 17*13$

$\therefore 2000^{2019} (mod\ 221) = 5$

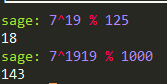
以上计算全程笔算可轻松完成，且与sage算出来的结果一致：

(2) 7^{1919}的最后三位是多少?

解：

1000 = 125*8

由中国剩余定理得：

$7^{1919} mod\ 1000 \cong ([7^{1919} mod\ 125],[7^{1919} mod\ 8])$

由欧拉定理

$7^{\phi(125)} = 7^{5^3 - 5^2} = 7^{100} ≡ 1\ mod\ 125$

$∴ 7^{1919} mod\ 125 = 7^{19} mod\ 125$

注意到 $7^3 = 343 ≡ -32\ (mod\ 125)$

$∴7^{19} = 7*(343^{6}) ≡ 7*((-32)^6) ≡ 7*(1024^3) ≡ 7*24^3 ≡ 18\ (mod\ 125)$

而 $7^{1919} ≡ (-1)^{1919} ≡ -1\ (mod\ 8)$

令

$x ≡ -1\ mod\ 8$

$x ≡ 18\ mod\ 125$

再次运用中国剩余定理得：

$x ≡ 143\ (mod\ 125*8)$

$∴7^{1919} mod\ 1000 = 143$

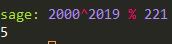
以上计算全程笔算可完成，且与sage算出来的结果一致：