粗略看了《商用密码——应用与安全性评估》的第一章和第三章（第三章没看完）

工程性太强了，过目即忘，便有此文

0. 前言

官方文档还没看呢，慢慢来……

1. SM2椭圆曲线公钥密码算法

其实在置顶文章已经写过了，我搬运一遍。

……

SM2、SM9是我国颁布的商用密码标准算法中的公钥密码算法，下面介绍SM2

Alice与Bob事先协商好相同的公开参数，包括p,n,E and G

其中p是大素数，E是定义在GF§上的椭圆曲线群，G是E的生成元

1.1. SM2数字签名算法

①密钥生成

a) 随机数 $d \in [1,n-2]$

b) 计算 $P = dG$ ，并将 P 作为公钥公开，d 作为私钥保存

②签名

a) Alice 选取随机数 $k \in [1,n-1]$ ，计算 $kG = (x_1,y_1)$

b) 计算 $r = (H(M)+x_1)\ mod\ n$ ，其中 $M = Z_A || m$ ，Z_A 是关于用户的可辨别标识、部分椭圆曲线系统参数和用户的公钥hash值，m是待签名信息，H为国家密码管理局核准的杂凑函数，如SM3；若 $r = 0\ mod\ n$ 或 $r + k = 0\ mod\ n$ ，则重新选取随机数 $k$

c) 计算 $s = (1+d)^{-1}(k-rd)\ mod\ n$ ; 若 $s \equiv 0$ ，则重新选取随机数 $k$ ，否则，将 $(r,s)$ 作为签名结果

③验签

a) Bob 收到 $M$ 和 $(r,s)$ 后，先检查 $r,s \in [1,n-1]$ 且 $r + s \neq 0\ mod\ n$ ；然后计算 $(x_1’,y_1’) = sG + (r+s)P$

b) 计算 $r' = (H(M)+x_1')\ mod\ n$ ；判断 r’ 与 r 是否相等，若相等则签名验证通过。

1.2. SM2密钥交换

	Alice	Bob
pk	$P_A$	$P_B$
sk	$d_A$	$d_B$
唯一标识	$Z_A$	$Z_B$

Alice:

1)选取随机数 $r_A \in [1,n-1]$ ，计算 $R_A = r_AG = (x_2,y_2)$ 并发送给Bob

Bob：

1)选取随机数 $r_B \in [1,n-1]$ ，计算 $R_B = r_BG = (x_3,y_3)$ 并发送给Alice

2)计算 $x_B = 2^w + (x_3 \land (2^w-1))$ 和 $t_B = (d_B + x_Br_B)\ mod\ n$

3)验证接收到的 $R_A$ 是椭圆曲线 $E$ 上的点，验证通过后计算 $x_A = 2^w + (x_2 \land (2^w-1))$

4)计算 $V = t_B(P_A + x_AR_A) = (x_V,y_V)$ ；若 V 是椭圆曲线 E 上的无穷远点，则重新选取 $r_B$

5)计算 $K_B = KDF(x_V||y_V||Z_A||Z_B,klen)$

Alice:

2)计算 $x_A = 2^w + (x_2 \land (2^w-1))$ 和 $t_A = (d_A+x_Ar_A)\ mod\ n$

3)验证接收到的 $R_B$ 是椭圆曲线上的点，验证通过后计算 $x_B = 2^w + (x_3 \land (2^w-1))$

4)计算 $U = t_A(P_B+x_BR_B) = (x_U,y_U)$ ; 若 U 是椭圆曲线 E 上的无穷远点，则重新选取 $r_A$ ,重新协商。

5)计算 $K_A = KDF(x_U||y_U||Z_A||Z_B,klen)$

经过以上协商，Alice与Bob共享密钥 $K_A = K_B$

1.3. SM2公钥加密算法

M：比特长度为mlen的明文

$Enc$

1）选取随机数 $l \in [1,n-1]$ , 分别计算 $C_1 = lG = (x_4,y_4)\ and\ lP = (x_5,y_5)$

2）计算 $e = KDF(x_5||y_5,mlen)$

3）计算 $C_2 = M \oplus e$ 和 $C_3 = H(x_5||M||y_5)$

4）输出密文 $C = C_1||C_3||C_2$

$Dec$

1）验证 $C_1$ 是否在椭圆曲线上，计算 $d*C_1 = (x_5,y_5)$

2）计算 $e = KDF(x_5||y_5,mlen)$

3）计算 $M = C_2 \oplus e$

4）计算 $C_3' = H(x_5||M||y_5)$ ，并验证 $C_3' = C_3$ 是否成立

输出明文 M

2. SM3密码杂凑算法

3. SM4分组密码算法

4. SM9标识密码算法

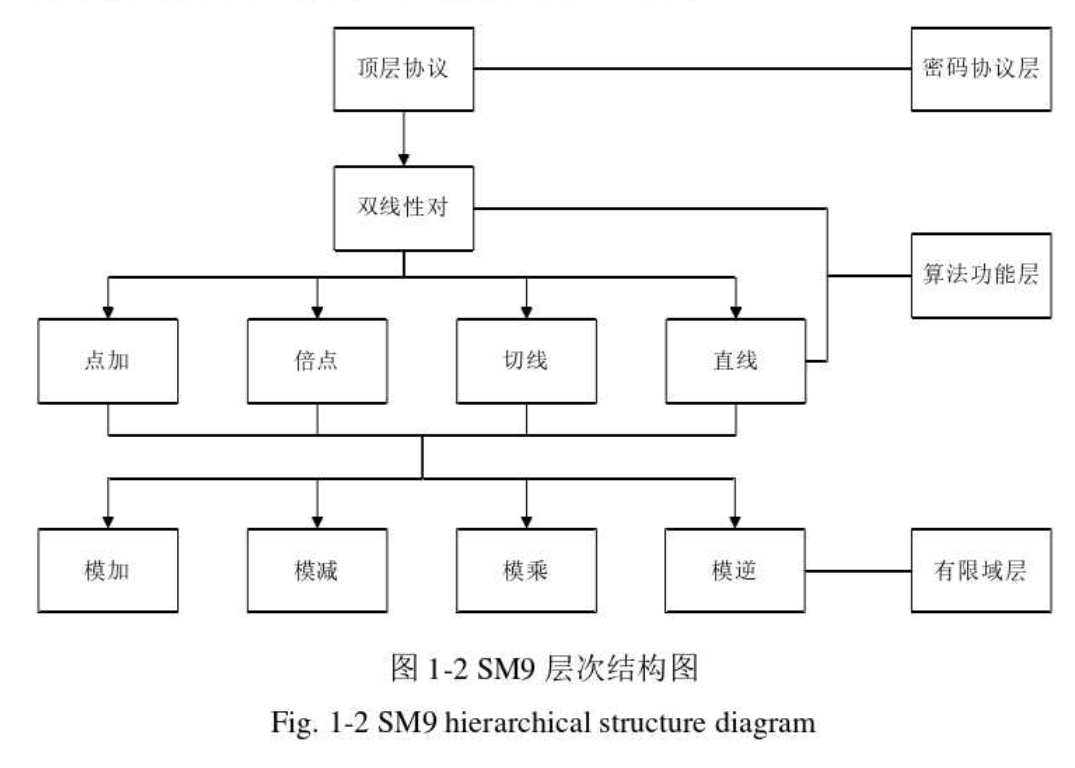
最近在实验室打工，负责研究有限域层运算

有限域层

有限域层包括有限域下的模加、模减、模乘、模逆。其中模乘占据SM9系统接近7成的运算量，因此模乘的效率改善尤为重要。

5. ZUC序列密码算法

参考

SM国产密码算法 — 晓鹿 (alienx.cn)

《商用密码——应用与安全性评估》